Contexte
De nombreux travaux attestent du caractère hydrophile des matrices organiques employées pour fabriquer les matériaux composites. Il est donc crucial d’étudier le processus de diffusion de l’humidité au sein de ces matériaux puisqu’il conduit à la fois à une chute des propriétés mécaniques et à des efforts mécaniques internes importants. Ces fortes contraintes internes peuvent alors favoriser un endommagement du matériau se manifestant par la fissuration du matériau. De plus, la physique complexe du problème est soumise à des incertitudes importantes qui doivent être prise en compte. Le projet vise à mettre en relation des approches numériques novatrices et performantes pour étudier le couplage entre la diffusion de l’eau et l’endommagement, le tout, dans un cadre aléatoire.
Ruptures scientifiques et innovation
La diffusion de l’eau dans les composites est déjà largement étudiée par de nombreuses équipes de recherche qui s’accordent à dire que son impact est néfaste sur le matériau. Toutefois, si des résultats expérimentaux existent, on ne trouve pas de méthodes numériques performantes associées à des modèles pertinents qui permettent de prédire le comportement de la structure en service. Ce projet permettra des avancées sur le développement de ces modèles et méthodes. Par ailleurs, l’ensemble des outils proposés seront étendus au cadre aléatoire afin de prendre en compte les incertitudes sur les phénomènes physiques ou la géométrie et le chemin de propagation des fissures. De telles approches permettront de caractériser au sens probabiliste, sous forme de lois de probabilité ou d’information statistique, des quantités d’intérêt cruciales dans le dimensionnement des structures EMR. Elles permettront également de mieux comprendre le couplage entre la diffusion de l’eau et l’usure des composites.
Impact technique et économique attendu
Les structures EMR sont dorénavant grandement composées de matériaux composites à matrice organique ayant d’excellentes propriétés mécaniques mais qui peuvent être endommagées par les diverses attaques de l’environnement marin. L’objectif du projet est de développer des outils numériques à l’usage des ingénieurs qui permettront d’étudier l’impact de la diffusion de l’eau sur l’endommagement de ces matériaux. Ces outils permettront d’optimiser la durée de vie des structures EMR et de réduire le coût de l’énergie produite.
Dates clés du projet
- Octobre 2016 - Début du projet
- Octobre 2018 - fin développement modèle hygroscopique déterministe et stochastique avec fissure
- Juin 2019 - fin développement modèle hygro-élastique déterministe et stochastique avec fissure
- Juin 2020 - fin développement modèle hygro-élastique déterministe et stochastique avec propagation de fissure
Démonstrateur
Développement d’outils numériques pour l’analyse de l’endommagement des matériaux composites utilisés dans les structures EMR.
Résultats
Campagne expérimentale sur l’endommagement de matériaux composites EMR en condition humide :
La campagne expérimentale avait pour objectif d’étudier le comportement hydrique d’échantillons composites verre/epoxy à des niveaux d’endommagement différents. Pour cela un protocole a été mis en place et une enceinte dédiée à ces échantillons a été créée (cf. figure 1-gauche). Parmi les résultats obtenus, nous avons constaté que le niveau d’endommagement modifiait le comportement hydrique (vitesse de diffusion et capacité maximale d’absorption) comme les montre la figure 1-droite. Les coefficients de diffusion ainsi que les capacités maximales d’absorption ont été identifiés à l’aide d’un algorithme de recherche développé sous Matlab©.
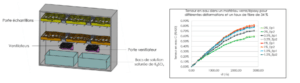
Figure 1 : (gauche) modèle CAO de l’enceinte développée pour le vieillissement et (droite) courbes de sorption obtenues pour des échantillons à différents niveaux d’endommagement.
L’étude a montré que ces paramètres augmentaient avec le niveau d’endommagement : la présence de fissure influe sur le coefficient de diffusion tandis que l’augmentation de la capacité maximale d’absorption est plus vraisemblablement due à la présence de porosité (cf. figure 2).

Figure 2 : (gauche) observation au MEB avec fissure et (droite) observation au MEB de porosité sur échantillons verre/époxy du projet.
Modèle hygroscopique déterministe et stochastique avec prise en compte de fissures :
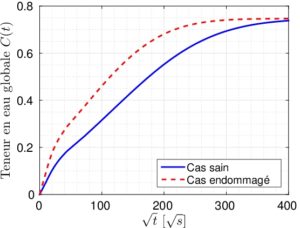
Ce premier travail avait pour objectif de mettre en place le modèle hygroscopique prenant en compte des fissures dites « débouchantes » au travers desquelles la diffusion de l’eau peut s’effectuer. La résolution de ce type de problème nécessitait la mise en place de méthodes numériques dédiées. Afin de s’affranchir notamment des problèmes de remaillage, la méthode des éléments finis étendus (X-FEM) a été retenue et adaptée aux spécificités du problème en utilisant une technique de pénalité et des fonctions d’enrichissement permettant d’imposer une teneur en eau le long de la fissure et de capturer les irrégularités de la solution au travers du front de fissure. La figure 1 présente des illustrations de champs de teneur en eau d’un composite verre/époxy pendant le régime transitoire au même instant pour un cas sans fissure et un cas avec fissure. On constate que la diffusion de l’eau au sein du matériau est nettement plus avancée pour le cas avec fissure. La figure 2 présente une comparaison de cinétiques de sorption (évolution de la teneur en eau globale avec le temps) pour ces deux mêmes cas. On peut observer une diffusion nettement plus rapide dans le cas avec fissure.
Figure 3 : comparaison des champs de teneur en eau [%H20] pour un composite verre epoxy sans fissure (gauche) et avec fissure (droite).
Figure 4 : courbes de sorption obtenues par simulation pour un cas sain (sans fissure) et endommagé (avec fissure).
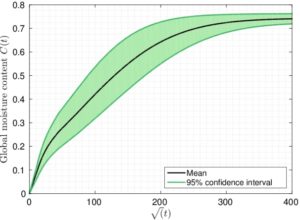
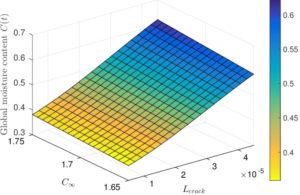
Le problème a ensuite été étendu au cadre stochastique au travers d’une modélisation probabiliste dans laquelle la variabilité est représentée par un ensemble fini de variables aléatoires. La propagation des incertitudes, consistant à déterminer les incertitudes en sortie du modèle en fonction des incertitudes d’entrée, est réalisée à l’aide d’approches spectrales stochastiques consistant à rechercher la solution sous forme fonctionnelle. Ce type de méthode se révèle efficace lorsque le nombre de variables aléatoires d’entrée est assez peu élevé. L’approche proposée a fait l’objet de développements spécifiques afin de s’adapter au cadre de ces approches. Des exemples de résultats sont donnés sur les figures 3 et 4. Dans ce problème la longueur de fissure ainsi que la capacité maximale d’absorption sont représentées à l’aide de variables aléatoires. L’aléa sur la longueur de fissure a été choisi important (coefficient de variation de 45%) comme souvent constaté tandis que celui sur la capacité maximale d’absorption est nettement plus faible (coefficient de variation de 5%). La figure 3 présente la courbe de sorption aléatoire du problème l’aide de sa moyenne et d’un intervalle de confiance à 95%. Sur cette même figure est illustrée la surface de réponse de ce processus aléatoire à un instant donné où la dispersion est importante.
Figure 5 : courbe de sorption aléatoire (gauche) et surface de réponse pour un temps donné (droite).
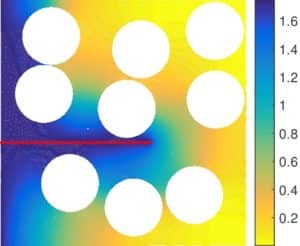
On peut observer que la variabilité sur la longueur de fissure a un impact beaucoup plus important que la variabilité sur la capacité maximale d’absorption. La figure 4 présente un post-traitement de la solution stochastique conduisant à une évaluation rapide des champs de teneur en eau pour différentes réalisations aléatoires de la longueur de fissure et de la capacité maximale d’absorption. On constate que, comme précédemment, plus la fissure est grande et plus la diffusion de l’eau est avancée.
Figure 6 : exemples de champs de teneur en eau local pour deux longueurs de fissures obtenus par post-traitement de la solution stochastique.
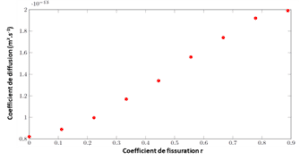
L’approche proposée a également permis de déterminer l’évolution du coefficient de diffusion effectif en fonction de la longueur de fissure en considérant le domaine d’étude comme un volume élémentaire représentatif. Deux cas ont été étudiés : le cas d’une résine époxy seule en présence d’une fissure et le cas d’un composite verre/époxy en présence d’une fissure. La figure 5 illustre les résultats pour ces deux cas. On constate une augmentation importante de ce coefficient de diffusion effectif dans les deux cas. Ce type de résultat pourra être utilisé dans des simulations à des échelles homogènes équivalentes.
Figure 5: évolution du coefficient de diffusion effectif en fonction du coefficient de fissuration (analogue à une densité de fissure) pour le cas d’une résine époxy seule (gauche) et d’un composite verre/époxy (droite).
Modèle hygro-élastique déterministe et stochastique avec prise en compte de fissure :
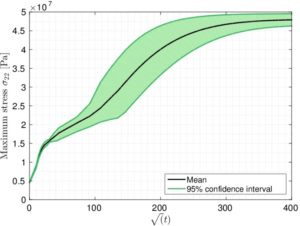
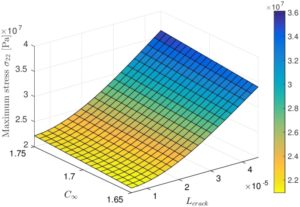
Dans cette partie, l’objectif était de prendre en compte la déformation hygroscopique provenant de la diffusion de l’eau dans le calcul élastique. Pour se faire, la méthode X-FEM a été adaptée afin de prendre en compte les résultats issus du calcul hygroscopique illustrée dans la partie précédente. Les illustrations suivantes sont issues d’une étude stochastique sur le même composite verre/époxy que dans la partie précédente. La figure 6 présente l’évolution de la contrainte maximale verticale aléatoire ainsi que sa surface de réponse en fonction de la longueur de fissure et la capacité maximale d’absorption.On peut observer une dispersion importante sur les résultats provenant principalement de l’aléa sur la longueur de la fissure.
Figure 6 : évolution de la contrainte maximale verticale aléatoire (gauche) et surface de réponse pour un temps donné (droite).
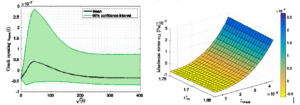
Figure 7 : évolution de l’ouverture de fissure aléatoire (gauche) et surface de réponse à un instant donné (droite).
Modèle hygro-élastique déterministe et stochastique avec propagation de fissure :
Dans cette dernière partie, nous avons amélioré le modèle proposé afin de prendre en compte la propagation d’une fissure pendant le vieillissement. Une étude déterministe a été proposée afin de comparer un calcul hygro-élastique avec et sans propagation de fissure. La figure 8 présente l’évolution de champ de teneur en eau en fonction de la propagation de la fissure issue de la diffusion de l’eau au sein du matériau composite verre/epoxy.

Figure 8 : évolution du champ de teneur en eau en parallèle de la propagation de la fissure
La figure 9 présente des comparaisons entre un calcul sans propagation de fissure et avec propagation de fissure. On constate tout d’abord que la teneur en eau globale est très affectée par la propagation de la fissure avec une vitesse de diffusion plus importante et une saturation atteinte plus tôt que dans le cas sans propagation de fissure. De plus, on observe sur la figure 69droite une ouverture de fissure beaucoup plus importante et plus rapide pour le cas avec propagation de fissure.
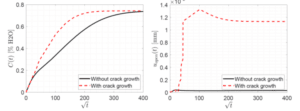
Figure 9 : comparaison entre un cas sans propagation de fissure et avec propagation de fissure : (gauche) comparaison de l’évolution de la teneur en eau globale et (droite) évolution de l’ouverture maximale de fissure.
Enfin, nous avons proposé une étude stochastique du comportement des paramètres pilotant la propagation de la fissure : l’angle de propagation de la fissure et l’augmentation de sa longueur notamment. Les figures 10 et 11 présentent quelques résultats stochastiques, sous forme de processus et de surfaces de réponse caractéristiques, pour ces 2 quantités en considérant la longueur de la fissure ainsi que la capacité maximale d’absorption comme des variables aléatoires.
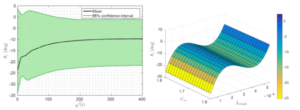
Figure 10 : évolution de l’angle de propagation de la fissure θC : (gauche) processus stochastique avec moyenne et intervalle de confiance et (droite) surface de réponse caractéristique en fonction de la longueur de la fissure Lcrack et de la capacité maximale d’absorption C∞.
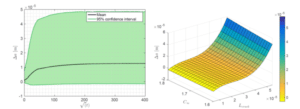
Figure 11 : évolution de l’augmentation de la longueur de fissure Δa : (gauche) processus stochastique avec moyenne et intervalle de confiance et (droite) surface de réponse caractéristique en fonction de la longueur de la fissure Lcrack et de la capacité maximale d’absorption C∞.
Sur chacune de ces deux dernières figures, on peut observer une variabilité très importante comme l’indique les très larges intervalles de confiance. Une légère distinction est toutefois à noter : en effet, comme le montre les surfaces de réponse, cette variabilité provient presque exclusivement de l’aléa sur la longueur de la fissure pour l’angle de propagation alors que celui sur la capacité maximale d’absorption joue un rôle non négligeable sur la variabilité de l’augmentation de la longueur de la fissure.
Publications et communications produites
Communications orales
- Stochastic study of the hygro-elastic behavior of composite materials: application to the durability of renewable marine energy structures, Clément, A., Bhati, G., Fréour, S. et Jacquemin, F. , 54th ESReDA Seminar on Risk, Reliability and Safety of Energy Systems In Coastal and Marine Environments, April 25 – 26, Nantes. (2018).
- Multiphysics modeling of the hygro-mechanical behavior of composites used in Marine Renewable Energy structures, A. Clément, A. Uguen, Q. Dézulier, S. Fréour, F. Jacquemin (GeM, Research Institute in Civil and Mechanical Engineering, CNRS UMR 6183, Nantes University, Centrale Nantes, France) – French American Innovation Day 2019 – Télécharger le poster
- Study of the hygro-elastic behavior of composite materials in presence of cracks: application to the durability of renewable marine energy structures, A. UGUEN, A. CLEMENT, S. FREOUR, F. JACQUEMIN, European Mechanics Society Colloquium 607 on Marine Aging of Polymers, Brest France, August 28th-29th 2019.
- Characterization and modelling of coupled hygro-thermo-mechanical behaviour of composites in harsh environment, A. CLEMENT, OPIN Workshop, Advanced Materials and Manufacturing (composite focus), 12 Novembre 2019, technocampus OCEAN, Bouguenais – France.
- Numerical stochastic study of damaged composite materials in humid environment, A. CLEMENT, S. FREOUR, F. JACQUEMIN. JOINT EVENT: ICCS23 – 23rd International Conference on Composite Structures & MECHCOMP6 – 6th International Conference on Mechanics of Composites, 1-4 septembre 2020, Université de Porto, Portugal (communication orale sans acte).